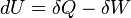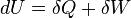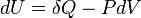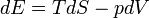Path function and Point function are introduced to identify the variables of thermodynamics.
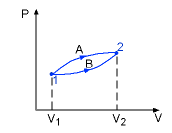

- Path function: Their magnitudes depend on the path followed during a process as well as the end states. Work (W), heat (Q) are path functions.
Process A: WA = 10 kJ
Process b: WB = 7 kJ
- Point Function: They depend on the state only, and not on how a system reaches that state. All properties are point functions.
Process A: V2 - V1 = 3 m3
Process B: V2 - V1 = 3 m3
Heat:-
Heat is energy transferred from one system to another solely by reason of a temperature difference between the systems. Heat exists only as it crosses the boundary of a system and the direction of heat transfer is from higher temperature to lower temperature.
For thermodynamics sign convention, heat transferred to a system is positive; Heat transferred from a system is negative.
The heat needed to raise a object's temperature from T1 to T2 is:
Q = cp m (T2 - T1)
where
cp = specific heat of the object (will be introduced
in the following section)
m = mass of the object
Unit of heat is the amount of heat required to cause a unit rise in temperature of a unit mass of water at atmospheric pressure.
- Btu: Raise the temperature of 1 lb of water 1 oF
- Cal: Raise the temperature of 1 gram of water 1 oC
J is the unit for heat in the S.I. unit system. The relation between Cal and J is
1 Cal = 4.184 J
Notation used in this book for heat transfer:
- Q : total heat transfer
 : the rate of heat transfer (the amount of heat transferred per unit time)
: the rate of heat transfer (the amount of heat transferred per unit time)- δQ: the differential amounts of heat
- q: heat transfer per unit mass
Modes of Heat Transfer: -
Conduction: Heat transferred between two bodies in direct contact.
Fourier's law:


If a bar of length L was put between a hot object TH and a cold object TL , the heat transfer rate is:

where
kt = Thermal conductivity of the bar
A = The area normal to the direction of heat
transfer
Convection: Heat transfer between a solid surface and an adjacent gas or liquid. It is the combination of conduction and flow motion. Heat transferred from a solid surface to a liquid adjacent is conduction. And then heat is brought away by the flow motion.
Newton's law of cooling:

where
h = Convection heat transfer coefficient
Ts = Temperature of the solid surface
Tf = Temperature of the fluid
The atmospheric air motion is a case of convection. In winter, heat conducted from deep ground to the surface by conduction. The motion of air brings the heat from the ground surface to the high air.
Radiation:  The energy emitted by matter in the form of electromagnetic waves as a result of the changes in the electronic configurations of the atoms or molecules.
The energy emitted by matter in the form of electromagnetic waves as a result of the changes in the electronic configurations of the atoms or molecules.
Stefan - Boltzmann law:

where
σ = Stefan - Boltzmann constant
ε = emissivity
Ts = Surface temperature of the object
Solar energy applications mainly use radiation energy from the Sun.

The three modes of heat transfer always exist simultaneously. For example, the heat transfer associated with double pane windows are:
- Conduction: Hotter (cooler) air outside each pane causes conduction through solid glass.
- Convection: Air between the panes carries heat from hotter pane to cooler pane.
- Radiation: Sunlight radiation passes through glass to be absorbed on other side.
Please view heat transfer books for details of modes of heat transfer.
Work: -
Work is the energy transfer associated with a force acting through a distance.

Dot product means the distance along the force's direction. For example, if a car runs at a flat road, its weight does zero work because the weight and the moving distance have a 90o angle.
Like heat, Work is an energy interaction between a system and its surroundings and associated with a process.
In thermodynamics sign convection, work transferred out of a system is positive with respect to that system. Work transferred in is negative.
Units of work is the same as the units of heat.
Notation:
- W : total work
- δW: differential amount of work
- w: work per unit mass
 : Power, the work per unit time
: Power, the work per unit time
Expansion and Compression Work: -
A system without electrical, magnetic, gravitational motion and surface tension effects is called a simple compressible system. Only two properties are needed to determine a state of a simple compressible system.
Considering the gas enclosed in a piston-cylinder device with a cross-sectional area of the piston A.
Initial State:
Finial State:
Then a work between initial and final states is: Pressure P, Volume V. Let the piston moving ds in a quasi-equilibrium manner. The differential work done during this process is:
δW = F ds = P A ds = P dV
The total work done during the whole process (from state (P1,V1) to state (P2,V2)) is:

This quasi-equilibrium expansion process can be shown on a P-V diagram. The differential area dA is equal to P dV. So the area under the process curve on a P-V diagram is equal, in magnitude, to the work done during a quasi-equilibrium expansion or compression process of a closed system.
Heat and Work - A Path Function: -
There are many similarities between heat and work. These are
- The heat and work are both transient phenomena. The systems do not possess heat or work. When a system undergoes aa change, heat transfer or work done may occur.
- The heat and work are boundary phenomena. They are observed at the boundary of the system
- The heat and work represent the energy crossing the boundary of the system.
- The heat and work are path functions and hence they are inexact differentials. They are written as δQ and δW.